
The slope value should be common for both lines if the equations of lines are given in the slope-intercept form.In order to calculate the distance, we check whether the given equations of parallel lines are in slope-intercept form (i.e.The steps to calculate the distance between two lines are as follows: Steps to Calculate Distance Between Two Lines For skew lines, the distance between two skew lines is equal to the length of the perpendicular between the lines.For intersecting lines, the shortest distance between both the lines is eventually zero.For parallel lines, the distance between two parallel lines is the perpendicular distance from any point on one line to the other line.We come across various different sets of lines such as parallel lines, intersecting lines, or skew lines. The minimum distance between any two points lying on the lines is basically the distance between two straight lines. For non-linear functions, the rate of change of a curve varies, and the derivative of a function at a given point is the rate of change of the function, represented by the slope of the line tangent to the curve at that point.The distance between two lines can be measured with the help of the two points that are there on each of the lines. While this is beyond the scope of this calculator, aside from its basic linear use, the concept of a slope is important in differential calculus. Given the points (3,4) and (6,8) find the slope of the line, the distance between the two points, and the angle of incline: m = Given two points, it is possible to find θ using the following equation:
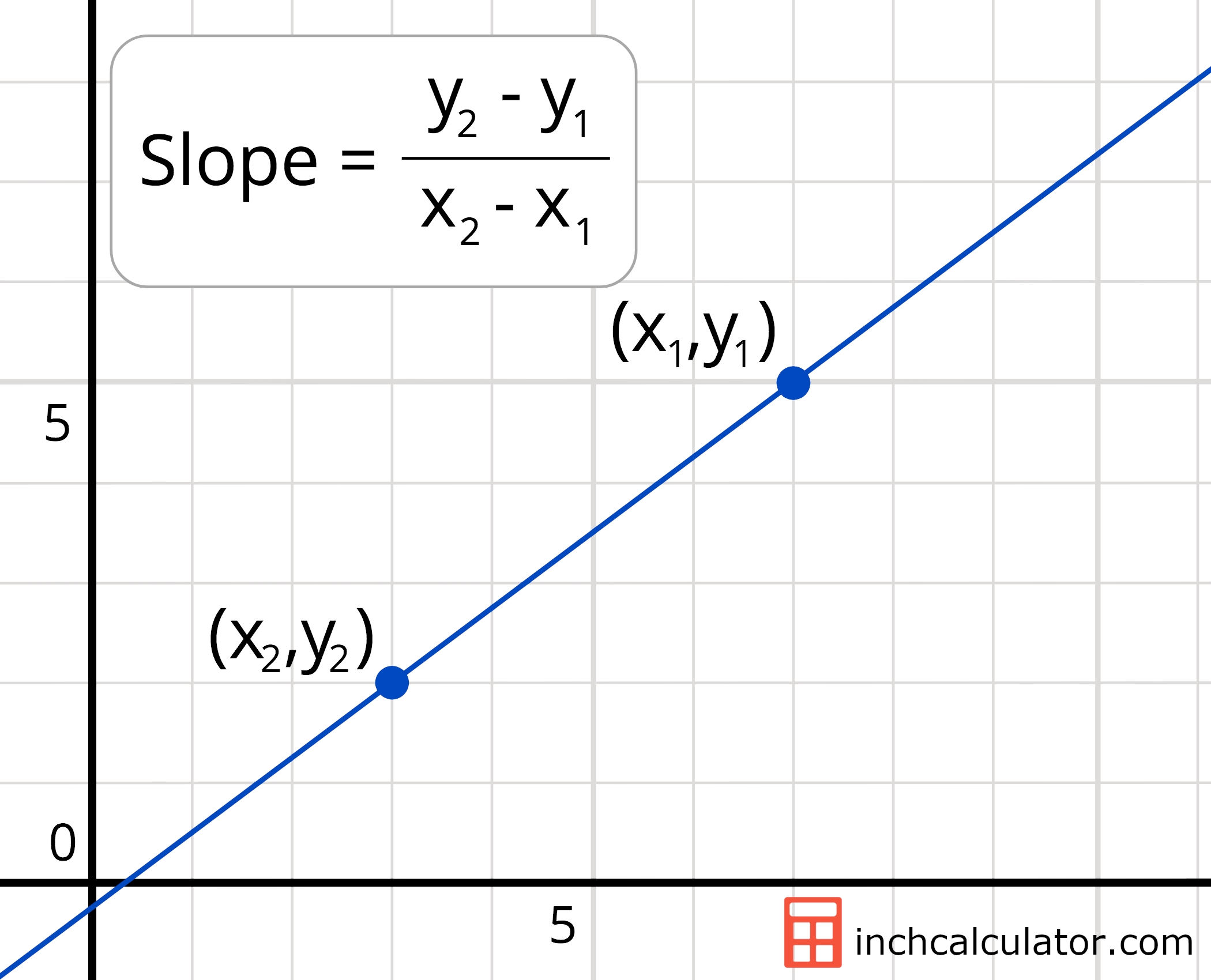

The above equation is the Pythagorean theorem at its root, where the hypotenuse d has already been solved for, and the other two sides of the triangle are determined by subtracting the two x and y values given by two points.
#SLOPE AND DISTANCE FORMULA GEOMETRY HOW TO#
Refer to the Triangle Calculator for more detail on the Pythagorean theorem as well as how to calculate the angle of incline θ provided in the calculator above. Since Δx and Δy form a right triangle, it is possible to calculate d using the Pythagorean theorem. It can also be seen that Δx and Δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x 1, y 1) and (x 2, y 2). In the equation above, y 2 - y 1 = Δy, or vertical change, while x 2 - x 1 = Δx, or horizontal change, as shown in the graph provided. The slope is represented mathematically as: m = In the case of a road, the "rise" is the change in altitude, while the "run" is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth's curvature should be considered as a factor. Slope is essentially the change in height over the change in horizontal distance, and is often referred to as "rise over run." It has applications in gradients in geography as well as civil engineering, such as the building of roads. A vertical line has an undefined slope, since it would result in a fraction with 0 as the denominator.A line has a constant slope, and is horizontal when m = 0.



 0 kommentar(er)
0 kommentar(er)
